Simple ODE
## =============================================================================
## R-Code to solve example 3.1.2 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A simple ordinary differential equation model
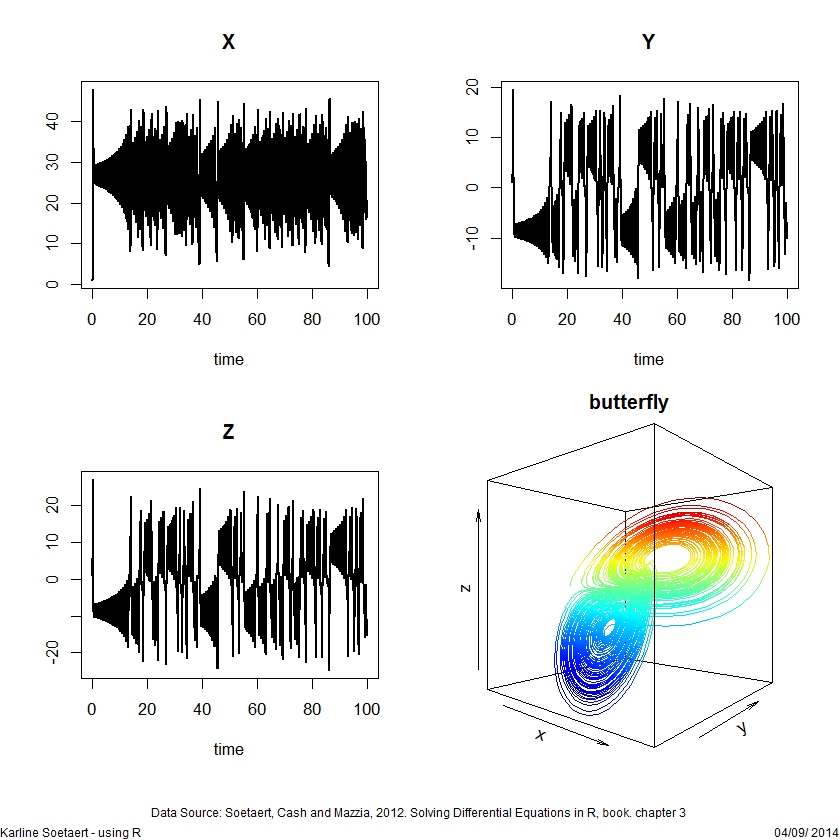
a <- -8/3 ; b <- -10; c <- 28
yini <- c(X = 1, Y = 1, Z = 1)
Lorenz <- function (t, y, parms) {
with(as.list(y), {
dX <- a * X + Y * Z
dY <- b * (Y - Z)
dZ <- -X * Y + c * Y - Z
list(c(dX, dY, dZ))
})
}
times <- seq(from = 0, to = 100, by = 0.01)
out <- ode(y = yini, times = times, func = Lorenz, parms = NULL)
plot(out, lwd = 2)
library(plot3D)
pm <- par (mar = c(1, 1, 1, 1))
lines3D(out[,"X"], out[,"Y"], out[,"Z"], colkey = FALSE,
colvar = out[,"Z"], bty = "f", main = "butterfly",
phi = 0)
par (mar = pm)ODE events
## =============================================================================
## R-Code to solve example 3.4.1.2 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## An ordinary differential equation model with events
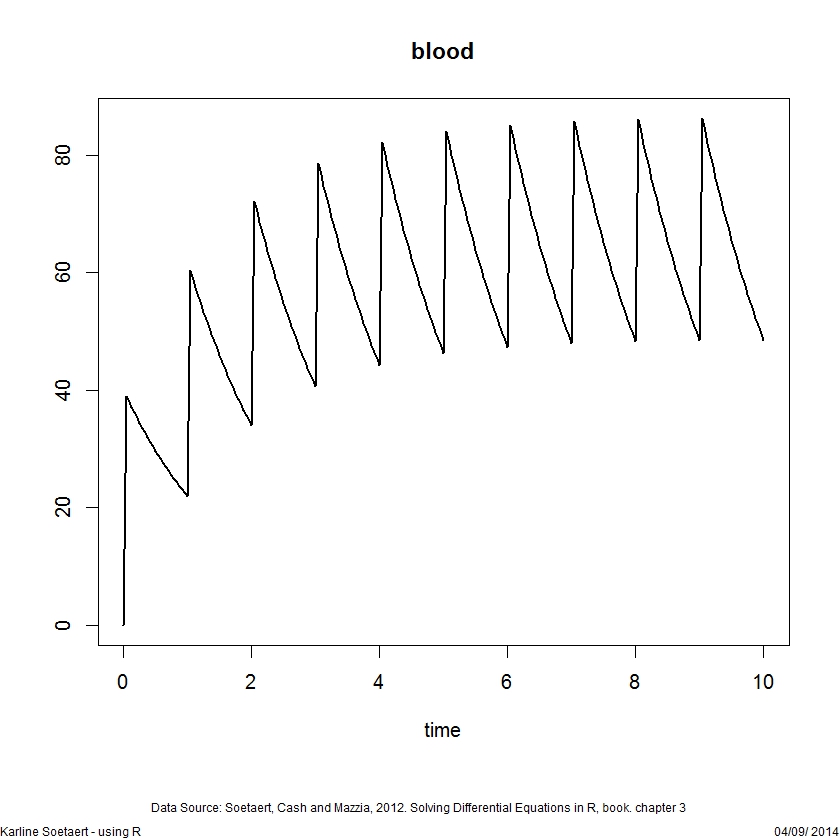
b <- 0.6
yini <- c(blood = 0)
pharmaco2 <- function(t, blood, p) {
dblood <- - b * blood
list(dblood)
}
injectevents <- data.frame(var = "blood",
time = 0:20,
value = 40,
method = "add")
head(injectevents, n=3)
times <- seq(from = 0, to = 10, by = 1/24)
out2 <- ode(func = pharmaco2, times = times, y = yini,
parms = NULL, method = "impAdams",
events = list(data = injectevents))
plot(out2, lwd = 2)ODE forcings
## =============================================================================
## R-Code to solve example 3.3.2 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
##
## An ordinary differential equation model with forcing functions
## The ozone model - needs file "light.rda"
## implemented by Karline Soetaert
## =============================================================================
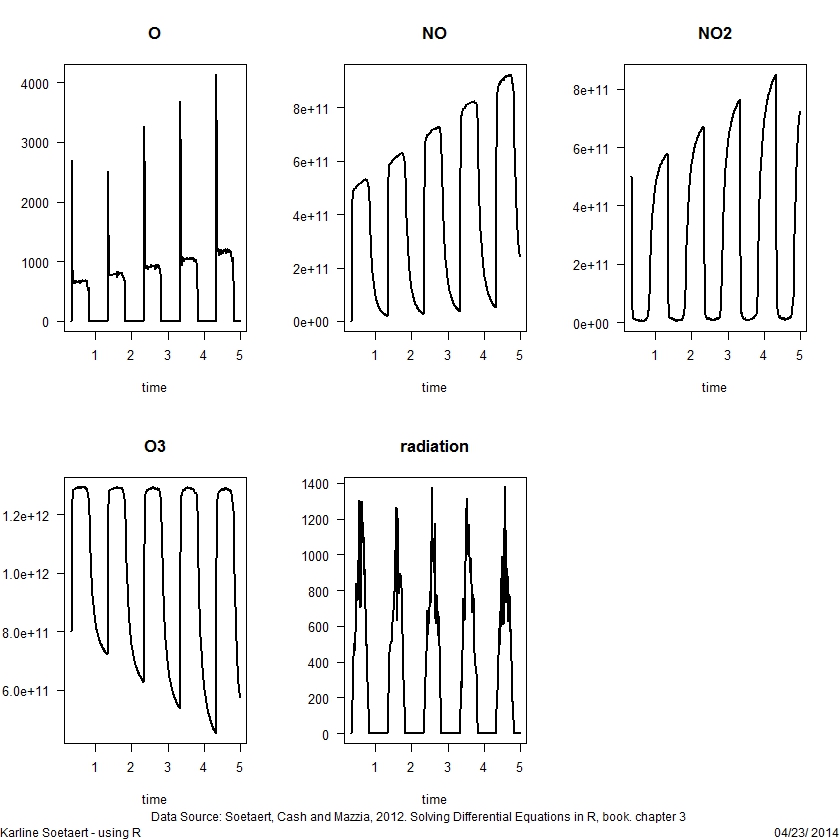
library (deSolve)
load(file = "light.rda") # contains data.frame Light
head(Light, n = 4)
irradiance <- approxfun(Light)
irradiance(seq(from = 0, to = 1, by = 0.25))
k3 <- 1e-11; k2 <- 1e10; k1a <- 1e-30
k1b <- 1; sigma <- 1e11
yini <- c(O = 0, NO = 1.3e8, NO2 = 5e11, O3 = 8e11)
chemistry <- function(t, y, parms) {
with(as.list(y), {
radiation <- irradiance(t)
k1 <- k1a + k1b*radiation
dO <- k1*NO2 - k2*O
dNO <- k1*NO2 - k3*NO*O3 + sigma
dNO2 <- -k1*NO2 + k3*NO*O3
dO3 <- k2*O - k3*NO*O3
list(c(dO, dNO, dNO2, dO3), radiation = radiation)
})
}
times <- seq(from = 8/24, to = 5, by = 0.01)
out <- ode(func = chemistry, parms = NULL, y = yini,
times = times, method = "bdf")
plot(out, type = "l", lwd = 2, las = 1)ODE roots
## =============================================================================
## R-Code to solve example 3.4.2 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## An ordinary differential equation model with root and events
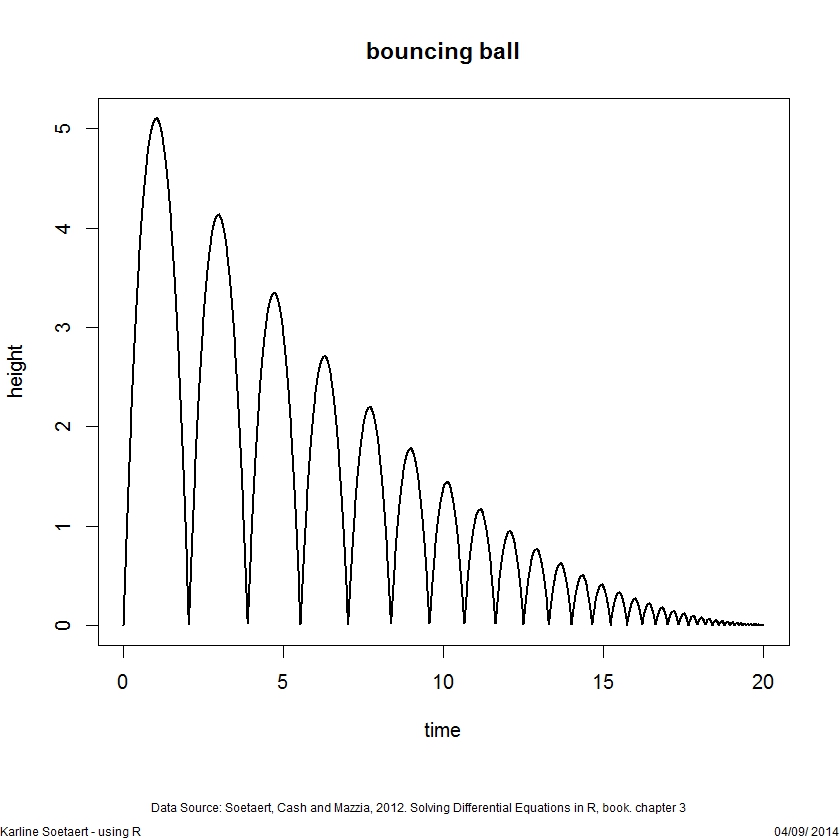
library(deSolve)
yini <- c(height = 0, velocity = 10)
ball <- function(t, y, parms) {
dy1 <- y[2]
dy2 <- -9.8
list(c(dy1, dy2))
}
rootfunc <- function(t, y, parms) y[1]
eventfunc <- function(t, y, parms) {
y[1] <- 0
y[2] <- -0.9*y[2]
return(y)
}
times <- seq(from = 0, to = 20, by = 0.01)
out <- ode(times = times, y = yini, func = ball,
parms = NULL, rootfun = rootfunc,
events = list(func = eventfunc, root = TRUE))
plot(out, which = "height", lwd = 2,
main = "bouncing ball", ylab = "height")DAE
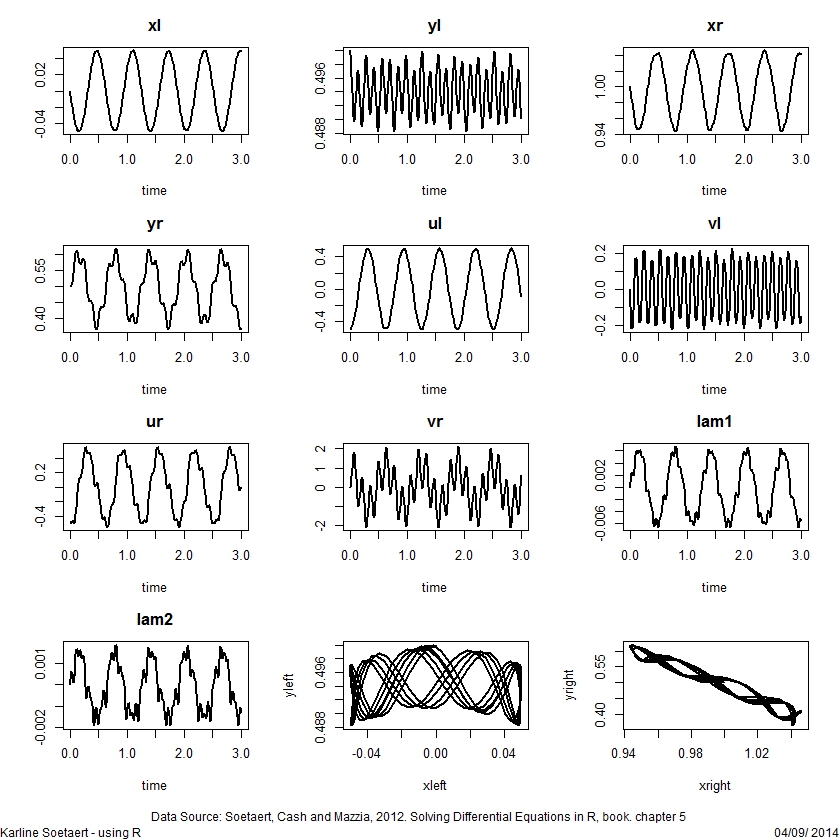
## =============================================================================
## R-Code to solve example 5.5.1 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A differential algebraic equation model
library(deSolve)
Caraxis <- function(t, y, dy, parms) {
with(as.list(y), {
f <- rep(0, 10)
yb <- r * sin(w * t)
xb <- sqrt(L^2 - yb^2)
Ll <- sqrt(xl^2 + yl^2)
Lr <- sqrt((xr - xb)^2 + (yr - yb)^2)
f[1:4] <- y[5:8]
f[5] <- 1/k*((L0-Ll)*xl/Ll + lam1*xb + 2*lam2*(xl-xr))
f[6] <- 1/k*((L0-Ll)*yl/Ll + lam1*yb + 2*lam2*(yl-yr)) -g
f[7] <- 1/k*((L0-Lr)*(xr - xb)/Lr - 2*lam2*(xl-xr))
f[8] <- 1/k*((L0-Lr)*(yr - yb)/Lr - 2*lam2*(yl-yr)) -g
f[9] <- xb * xl + yb * yl
f[10]<- (xl - xr)^2 + (yl - yr)^2 - L^2
delt <- dy - f
delt[9:10] <- -f[9:10]
list(delt)
})
}
eps <- 0.01; M <- 10; k <- M * eps * eps/2
L <- 1; L0 <- 0.5; r <- 0.1; w <- 10; g <- 9.8
yini <- c(xl = 0, yl = L0, xr = L, yr = L0,
ul = -L0/L, vl = 0, ur = -L0/L, vr = 0,
lam1 = 0, lam2 = 0)
library(deTestSet)
rootfun <- function (dyi, y, t)
unlist(Caraxis(t, y, dy = c(dyi, 0, 0),
parms = NULL)) [1:8]
dyini <- multiroot(f = rootfun, start = rep(0,8),
y = yini, t = 0)$root
(dyini <- c(dyini, 0, 0))
Caraxis(t = 0, yini, dyini, NULL)
index <- c(4, 4, 2)
times <- seq(from = 0, to = 3, by = 0.01)
out <- mebdfi(y = yini, dy = dyini, times = times,
res = Caraxis, parms = parameter, nind = index)
par(mar = c(4, 4, 3, 2))
plot(out, lwd = 2, mfrow = c(4,3))
plot(out[,c("xl", "yl")], xlab = "xleft", ylab = "yleft",
type = "l", lwd = 2)
plot(out[,c("xr", "yr")], xlab = "xright", ylab = "yright",
type = "l", lwd = 2)DAE mass
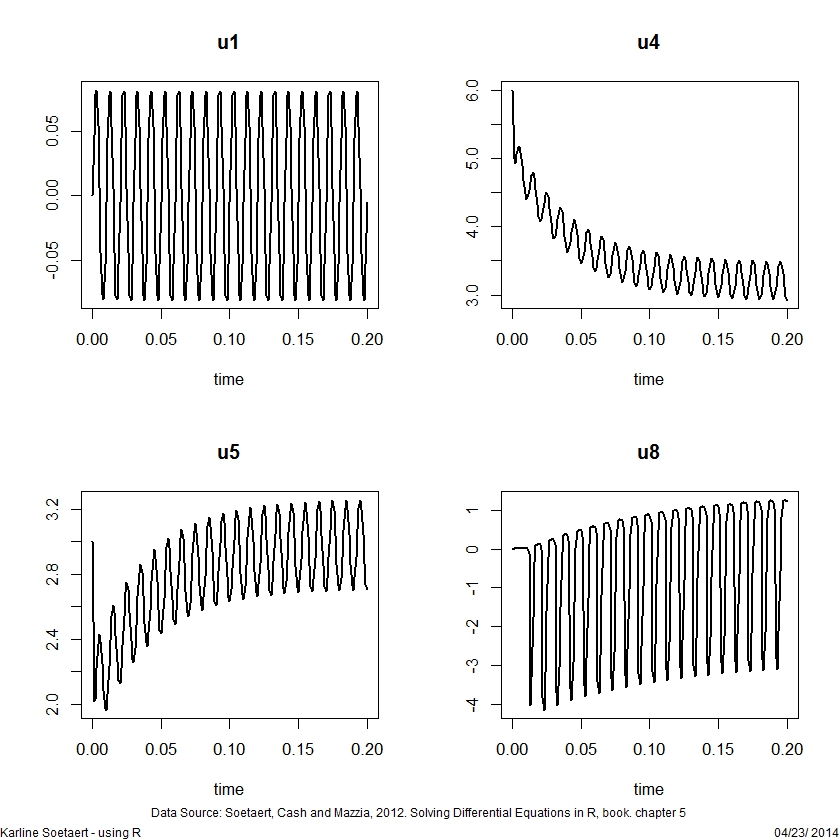
## =============================================================================
## R-Code to solve example 5.6.1 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
##
## A DAE model, solved in linearly implicit form
## The transistor amplifier
## implemented by Karline Soetaert
## =============================================================================
library(deSolve)
Transistor <- function(t, u, du, pars) {
delt <- vector(length = 8)
uin <- 0.1 * sin(200 * pi * t)
g23 <- beta * (exp( (u[2] - u[3]) / uf) - 1)
g56 <- beta * (exp( (u[5] - u[6]) / uf) - 1)
delt[1] <- (u[1] - uin)/R0
delt[2] <- u[2]/R1 + (u[2]-ub)/R2 + (1-alpha) * g23
delt[3] <- u[3]/R3 - g23
delt[4] <- (u[4] - ub) / R4 + alpha * g23
delt[5] <- u[5]/R5 + (u[5]-ub)/R6 + (1-alpha) * g56
delt[6] <- u[6]/R7 - g56
delt[7] <- (u[7] - ub) / R8 + alpha * g56
delt[8] <- u[8]/R9
list(delt)
}
ub <- 6; uf <- 0.026; alpha <- 0.99; beta <- 1e-6; R0 <- 1000
R1 <- R2 <- R3 <- R4 <- R5 <- R6 <- R7 <- R8 <- R9 <- 9000
C1 <- 1e-6; C2 <- 2e-6; C3 <- 3e-6; C4 <- 4e-6; C5 <- 5e-6
mass <- matrix(nrow = 8, ncol = 8, byrow = TRUE, data = c(
-C1,C1, 0, 0, 0, 0, 0, 0,
C1,-C1, 0, 0, 0, 0, 0, 0,
0, 0,-C2, 0, 0, 0, 0, 0,
0, 0, 0,-C3, C3, 0, 0, 0,
0, 0, 0, C3,-C3, 0, 0, 0,
0, 0, 0, 0, 0,-C4, 0, 0,
0, 0, 0, 0, 0, 0,-C5, C5,
0, 0, 0, 0, 0, 0, C5,-C5
))
yini <- c(0, ub/(R2/R1+1), ub/(R2/R1+1),
ub, ub/(R6/R5+1), ub/(R6/R5+1), ub, 0)
names(yini) <- paste("u", 1:8, sep = "")
ind <- c(8, 0, 0)
times <- seq(from = 0, to = 0.2, by = 0.001)
out <- radau(func = Transistor, y = yini, parms = NULL,
times = times, mass = mass, nind = ind)
plot(out, lwd = 2, which = c("u1", "u4", "u5", "u8"))DDE
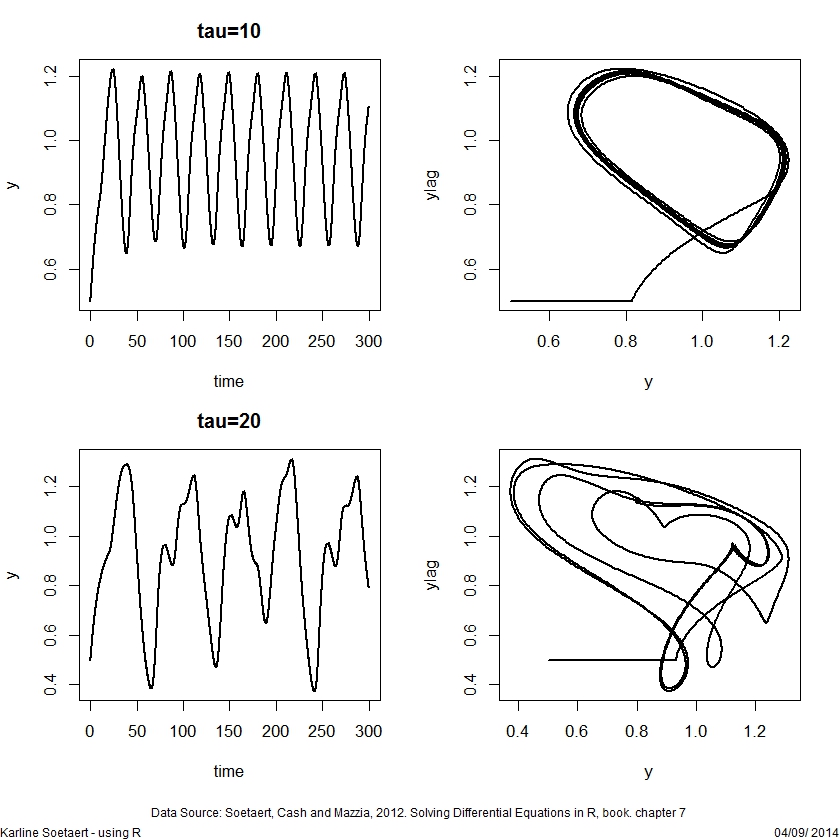
## =============================================================================
## R-Code to solve example 7.3 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A delay differential equation model
library(deSolve)
mackey <- function(t, y, parms, tau) {
tlag <- t - tau
if (tlag <= 0)
ylag <- 0.5
else
ylag <- lagvalue(tlag)
dy <- 0.2 * ylag * 1/(1+ylag^10) - 0.1 * y
list(dy = dy, ylag = ylag)
}
yinit <- 0.5
times <- seq(from = 0, to = 300, by = 0.1)
yout1 <- dede(y = yinit, times = times, func = mackey,
parms = NULL, tau = 10)
yout2 <- dede(y = yinit, times = times, func = mackey,
parms = NULL, tau = 20)
plot(yout1, lwd = 2, main = "tau=10",
ylab = "y", mfrow = c(2, 2), which = 1)
plot(yout1[,-1], type = "l", lwd = 2, xlab = "y")
plot(yout2, lwd = 2, main = "tau=20",
ylab = "y", mfrow = NULL, which = 1)
plot(yout2[,-1], type = "l", lwd = 2, xlab = "y")DDE events
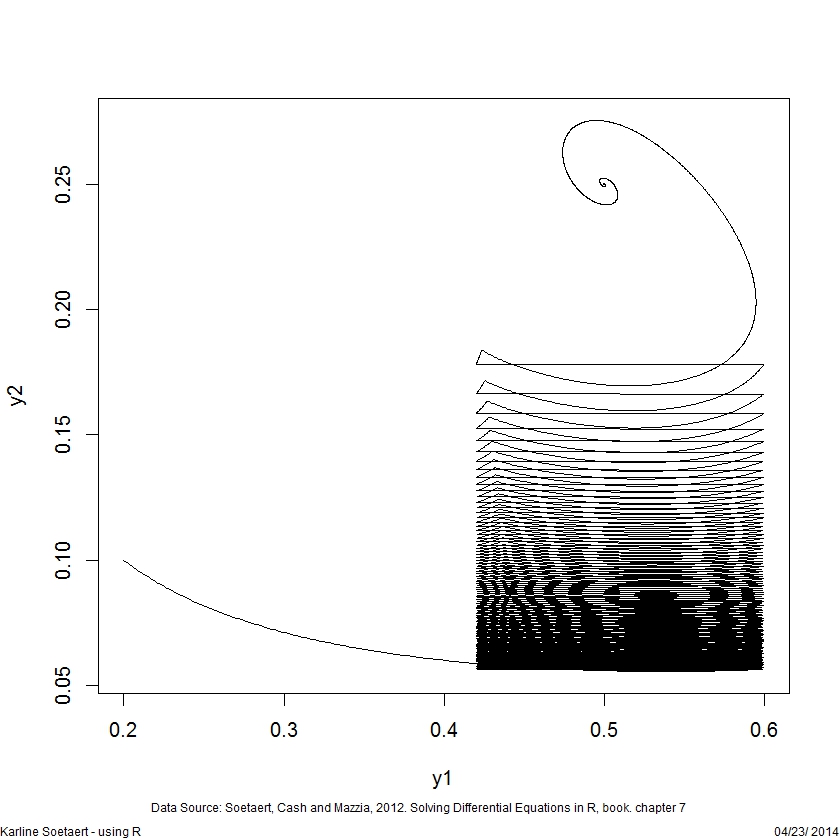
## =============================================================================
## R-Code to solve example 7.6 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
##
## A delay differential equation model
## Predator-prey with harvesting - takes a while
## implemented by Karline Soetaert
## -----------------------------------------------------------------------------
library(deSolve)
LVdede <- function(t, y, p) {
if (t > tau1) Lag1 <- lagvalue(t - tau1) else Lag1 <- yini
if (t > tau2) Lag2 <- lagvalue(t - tau2) else Lag2 <- yini
dy1 <- r * y[1] *(1 - Lag1[1]/K) - a*y[1]*y[2]
dy2 <- a * b * Lag2[1]*Lag2[2] - d*y[2]
list(c(dy1, dy2))
}
rootfun <- function(t, y, p)
return(y[1] - Ycrit)
eventfun <- function(t, y, p)
return (c(y[1] * 0.7, y[2]))
r <- 1; K <- 1; a <- 2; b <- 1; d <- 1; Ycrit <- 1.2*d/(a*b)
tau1 <- 0.2; tau2 <- 0.2
yini <- c(y1 = 0.2, y2 = 0.1)
times <- seq(from = 0, to = 200, by = 0.01)
yout <- dede(func = LVdede, y = yini, times = times,
parms = 0, rootfun = rootfun,
events = list(func = eventfun, root = TRUE))
attributes(yout)$troot [1:10]
plot(yout[,-1], type = "l")PDE
## =============================================================================
## R-Code to solve example 9.3.4 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A 3-D partial differential equation model
library(deSolve)
Nx <- 100
Ny <- 100
xgrid <- setup.grid.1D(-7, 7, N=Nx)
ygrid <- setup.grid.1D(-7, 7, N=Ny)
x <- xgrid$x.mid
y <- ygrid$x.mid
sinegordon2D <- function(t, C, parms) {
u <- matrix(nrow = Nx, ncol = Ny,
data = C[1 : (Nx*Ny)])
v <- matrix(nrow = Nx, ncol = Ny,
data = C[(Nx*Ny+1) : (2*Nx*Ny)])
dv <- tran.2D (C = u, C.x.up = 0, C.x.down = 0,
C.y.up = 0, C.y.down = 0,
D.x = 1, D.y = 1,
dx = xgrid, dy = ygrid)$dC - sin(u)
list(c(v, dv))
}
peak <- function (x, y, x0 = 0, y0 = 0)
exp(-((x-x0)^2 + (y-y0)^2))
uini <- outer(x, y,
FUN = function(x, y) peak(x, y, 2,2) + peak(x, y,-2,-2)
+ peak(x, y,-2,2) + peak(x, y, 2,-2))
vini <- rep(0, Nx*Ny)
times <- 0:3
print(system.time(
out <- ode.2D (y = c(uini, vini), times = times,
parms = NULL, func = sinegordon2D,
names = c("u", "v"),
dimens = c(Nx, Ny), method = "ode45")
))
mr <- par(mar = c(0, 0, 1, 0))
image(out, main = paste("time =", times), which = "u",
grid = list(x = x, y = y), method = "persp",
border = NA, col = "grey", box = FALSE,
shade = 0.5, theta = 30, phi = 60, mfrow = c(2, 2),
ask = FALSE)
par(mar = mr)PDE imaginary
## =============================================================================
## R-Code to solve example 9.3.4 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A partial differential equation model with complex numbers
library(deSolve)
alf <- 0.5
gam <- 1
Schrodinger <- function(t, u, parms) {
du <- 1i * tran.1D (C = u, D = 1, dx = xgrid)$dC +
1i * gam * abs(u)^2 * u
list(du)
}
N <- 300
xgrid <- setup.grid.1D(-20, 80, N = N)
x <- xgrid$x.mid
c1 <- 1
c2 <- 0.1
sech <- function(x) 2/(exp(x) + exp(-x))
soliton <- function (x, c1)
sqrt(2*alf/gam) * exp(0.5*1i*c1*x) * sech(sqrt(alf)*x)
yini <- soliton(x, c1) + soliton(x-25, c2)
times <- seq(0, 40, by = 0.1)
print(system.time(
out <- ode.1D(y = yini, parms = NULL, func = Schrodinger,
times = times, dimens = 300, method = "adams")
))
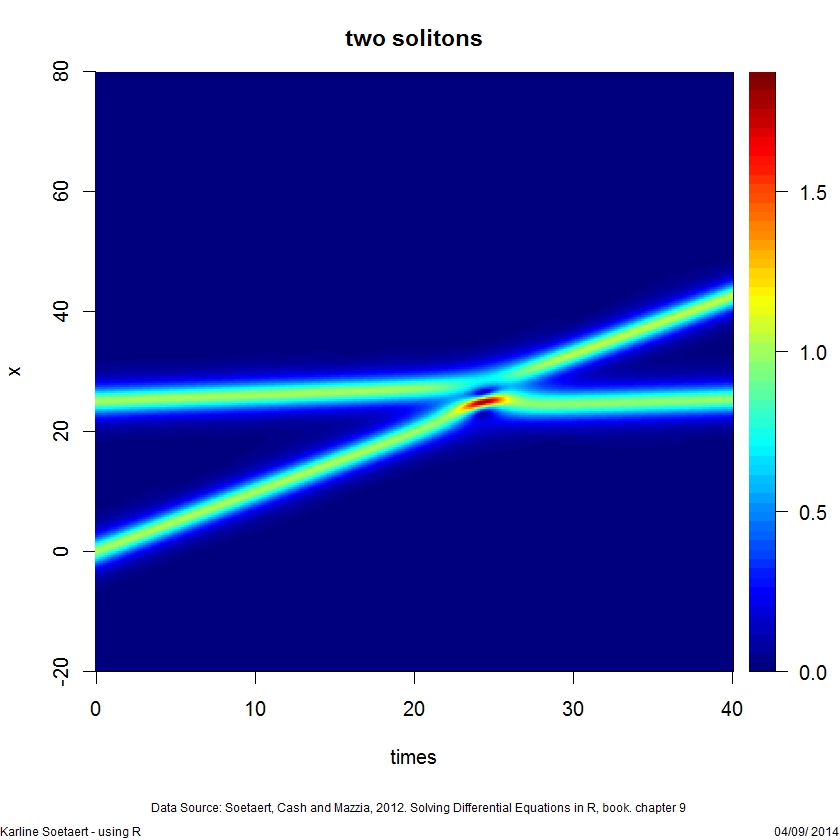
image(abs(out), grid = x, ylab = "x", main = "two solitons",
legend = TRUE)BVP
## =============================================================================
## R-Code to solve example 11.3 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## A boundary value problem
library(bvpSolve)
swirl <- function (t, Y, eps) {
with(as.list(Y),
list(c((g*f1 - f*g1)/eps,
(-f*f3 - g*g1)/eps))
)
}
eps <- 0.001
x <- seq(from = 0, to = 1, length = 100)
yini <- c(g = -1, g1 = NA, f = 0, f1 = 0, f2 = NA, f3 = NA)
yend <- c(1, NA, 0, 0, NA, NA)
Soltwp <- bvptwp(x = x, func = swirl, order = c(2, 4),
par = eps, yini = yini, yend = yend)
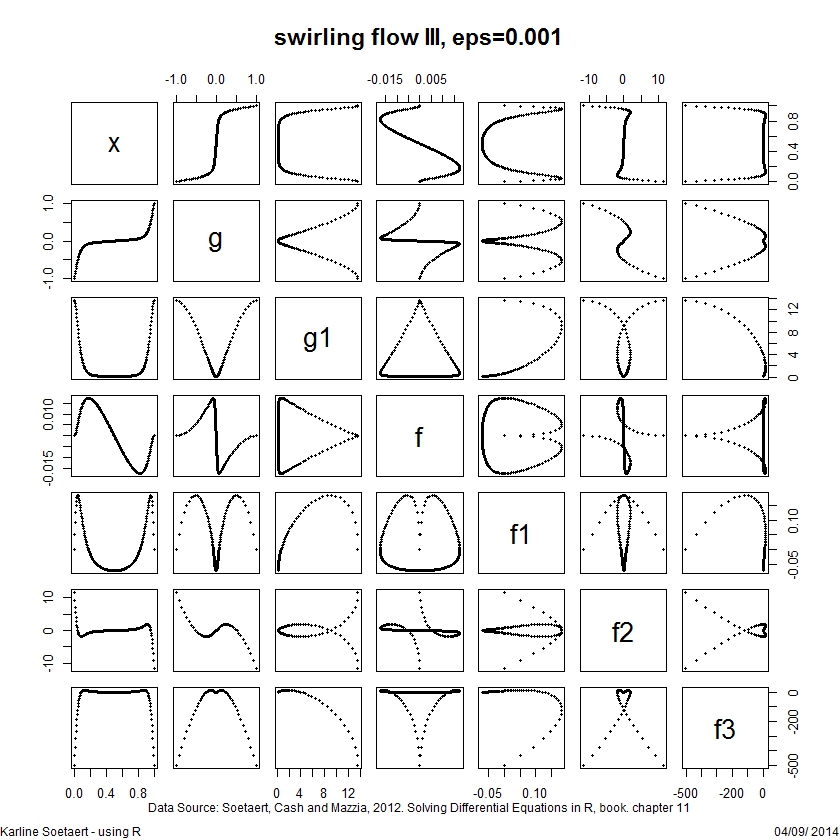
pairs(Soltwp, main = "swirling flow III, eps=0.001",
pch = 16, cex = 0.5)
diagnostics(Soltwp)BVP reaction transport
## =============================================================================
## R-Code to solve example 11.9 from the book
## K. Soetaert, J. Cash and F. Mazzia, 2012.
## Solving differential equations in R. UseR, Springer, 248 pp.
## http://www.springer.com/statistics/computational+statistics/book/978-3-642-28069-6.
## implemented by Karline Soetaert
## =============================================================================
## Steady-state solution of a reaction-transport problem
library(ReacTran)
N <- 1000
Grid <- setup.grid.1D(N = N, L = 100000)
v <- 1000; D <- 1e7; O2s <- 300
NH3in <- 500; O2in <- 100; NO3in <- 50
r <- 0.1; k <- 1.; p <- 0.1
Estuary <- function(t, y, parms) {
NH3 <- y[1:N]
NO3 <- y[(N+1):(2*N)]
O2 <- y[(2*N+1):(3*N)]
tranNH3<- tran.1D (C = NH3, D = D, v = v,
C.up = NH3in, C.down = 10, dx = Grid)$dC
tranNO3<- tran.1D (C = NO3, D = D, v = v,
C.up = NO3in, C.down = 30, dx = Grid)$dC
tranO2 <- tran.1D (C = O2 , D = D, v = v,
C.up = O2in, C.down = 250, dx = Grid)$dC
reaeration <- p * (O2s - O2)
r_nit <- r * O2 / (O2 + k) * NH3
dNH3 <- tranNH3 - r_nit
dNO3 <- tranNO3 + r_nit
dO2 <- tranO2 - 2 * r_nit + reaeration
list(c( dNH3, dNO3, dO2 ))
}
print(system.time(
std <- steady.1D(y = runif(3 * N), parms = NULL,
names=c("NH3", "NO3", "O2"),
func = Estuary, dimens = N,
positive = TRUE)
))
NH3in <- 100
std2 <- steady.1D(y = runif(3 * N), parms = NULL,
names=c("NH3", "NO3", "O2"),
func = Estuary, dimens = N,
positive = TRUE)
plot(std, std2, grid = Grid$x.mid, ylab = "mmol/m3", lwd = 2,
xlab = "m", mfrow = c(1,3), col = c("black", "red"))
legend("bottomright", lty = 1:2, title = "NH3in", lwd = 2,
legend = c(500, 100), col = c("black", "red"))